부모의 수학기대와 유아 수학 능력의 관계: 난이도에 따른 가정수학활동과 수학 사교육 의존도의 매개효과
The Relationship Between Parents’ Math Expectations and Children’s Math Achievements: Mediating Effects of Home Math Practices by Difficulty Level and Dependency on Private Math Education
Article information
Trans Abstract
Objectives
The study aim to examine the relationship between parents’ math expectations and young children’s math achievements by focusing on the mediating effects of home math practices according to difficulty level and dependency on private math education. Thus, an objective of the current study was to investigate the proper educational environment for enhancing young children’s math achievements.
Methods
A total of 297 children aged 4 and 5 years and their parents were included in the study. Parents were surveyed regarding the Home math environments and controlling variables. Home math practices were divided into basic and advanced math practices based on difficulty level. For the children, math achievements, such as numeracy and mathematical problem-solving skills, were assessed using the PENS-B and Woodcock-Johnson Ⅲ Applied Problems tests.
Results
Parent’s high levels of math expectations predicted a greater frequency of basic and advanced math practices at home; however, they did not predict a dependency on private math education. Additionally, advanced math practices at home partially mediated the association between parents’ math expectations and young children’s math achievements. Furthermore, the levels of basic math practices and dependency on private math education at home did not predict young children’s numeracy and mathematical problem-solving skills.
Conclusion
Findings of this study imply that to improve mathematical achievements in early childhood—including numeracy and mathematical problem-solving skills—, advanced practices with parents ar home is more beneficial than basic practices at home or private math education.
Introduction
유아기의 수학 능력은 언어능력과 함께 기초학업능력으로 분류되는데, 이는 수학 및 언어능력이 학령기 학업성취의 기반이 되는 주요 인지능력이기 때문이다(Curby & Chavez, 2013; Rabiner, Godwin, & Dodge, 2016). 이에 연구자들은 유아의 수학 및 언어능력 발달에 도움이 되는 요인에 대한 연구를 활발히 진행해 왔다. 부모가 제공하는 가정 환경 역시 유아의 발달 수준을 결정하는 요인으로 주요하게 다루어져야 할 환경이다. 애착관계를 기반으로 한 부모가 제공하는 수학적 혹은 언어적 상호작용은 유아로 하여금 해당 자극이 의미 있고 중요한 것이라고 인식하게 하며, 더욱 흥미를 갖게 한다. 그러나 지금까지 가정의 문해환경과 유아기 언어능력의 발달에 대한 연구가 매우 풍부하게 이루어져온 것에 비해, 가정의 수학 환경과 유아기 수학 능력 발달의 관계에 대한 연구는 상대적으로 그 양과 범위가 미비하다(Im, Choi, & Lee, 2019; Kang & Im, 2023; Skwarchunk, Sowinski, & LeFevre, 2014). 관련 연구들을 살펴보면, 부모가 제공하는 수학적 상호작용과 환경이 유아의 수학 능력에 미치는 영향(Kang & Im, 2023; H.-K. Lee & Park, 2010)과 유아기 자녀를 양육하는 어머니의 수학적 상호작용 및 가정의 수학 문해환경에 영향을 미치는 요인들(Hong, 2014; E. J. Lee & Kim, 2018; Oh & Kim, 2021)을 중심으로 연구가 이루어져 왔다. 연구자들은 유아기 자녀를 위한 가정의 수학환경에 대한 관심과 연구가 더욱 필요함을 역설하고 있다.
가정의 수학환경은 여러 요소로 구성되는데, 그 중 두 가지 주요 요인은 부모의 수학 기대와 가정수학활동이다(Kleemans, Segers, & Verhoeven, 2018). 부모의 수학 기대란, 자녀가 수와 관련된 기술을 어느 정도의 수준으로 숙달하길 바라는가를 의미한다(Segers, Kleemans, & Verhoeven, 2015). 부모의 수학 기대가 높을 때 가정에서 유아를 위한 수학 학습 기회를 더 자주 제공하는 것으로 나타난다. 예를 들면, 수학 기대가 높은 부모들은 자녀와 시계나 달력에 대해 이야기 나누기, 구체물을 이용해 수 세어보기, 간단한 덧셈 해 보기, 요리하며 수학적 요소 탐색하기 등과 같은 가정수학활동을 더 많이 하는 경향이 있다(Im et al., 2019; Susperreguy, Douglas, Xu, Molina-Rojas, & LeFevere, 2020). 즉, 자녀가 수학적 성취를 하는 것에 대한 기대가 높은 부모는 일상 속에서 경험하는 수학적 요인에 더욱 주목하고 자녀와 함께 상호작용하는 빈도가 높게 나타난다.
그러나 부모의 수학 기대가 가정수학활동에 미치는 영향력에 대해 살펴본 선행연구들은 대체로 가정수학활동을 부모와의 수학적 상호작용 빈도로 측정해, 가정수학활동의 유형을 세부적으로 살펴보는 데는 한계가 있었다(Im et al., 2019). 이러한 문제의식에 기반해, 가정수학활동을 난이도에 따라 기본수학활동과 고급수학활동으로 구분해 분석하고자 하는 시도가 있었다. 기본수학활동은 유아기에 할 수 있을 것으로 예측되는 난이도의 활동인 데 비해, 고급수학활동은 유아기에 기대되는 수준보다 약간 더 어려운 수준의 활동을 의미한다(Girard, Longo, Chesnokova, Epinat-Duclos, & Prado, 2023). 다양한 사회경제적 배경을 가진 유아들을 대상으로 포괄한 선행연구(del Río, Susperreguy, Strasser, & Salinas, 2017)는 어머니의 수학 기대 수준이 높을수록 난이도가 높은 수학활동을 더 많이 제공하는 경향이 있으며, 이로 인해 자녀의 수학적 수행 능력(numeracy performance)이 더 높게 나타남을 보여주었다. Susperreguy 등(2020)은 부모의 수학 기대가 기본수학활동 및 고급수학활동 정도를 모두 정적으로 예측하지만, 4세 유아기 자녀의 수 기술(early number skills)에 영향을 미치는 것은 고급수학활동이었음을 보고하였다. 이러한 분석 결과는 가정수학활동을 난이도에 따라 구분해 분석할 필요성을 보여주고 있으나, 부모의 수학 기대가 가정수학활동에 미치는 영향을 살펴본 연구 중 가정수학활동을 난이도에 따라 구분한 연구는 소수에 불과하며 국내 연구에서는 더욱 찾아보기 어렵다.
한편, 부모의 수학 기대가 높을수록 가정수학활동뿐 아니라 수학 사교육에 대한 의존도도 높아질 것으로 예상해볼 수 있다. 수학 사교육에 대한 의존도란, 부모가 유아의 수학 학습을 위한 방법으로 학습지나 학원과 같은 사교육에 의존하는 정도를 의미한다. 수학 사교육 의존도는 부모가 유아기 수학 사교육이 얼마나 중요하다고 믿는지, 그 효과가 얼마나 높다고 믿는지, 실제로 얼마나 수학 사교육을 이용하고 있는지 등을 검토함으로써 측정할 수 있다. 우리나라는 교육열이 높게 나타나는 국가로(K. Kim, 2016), 유아기부터 상당 비율의 아동이 수학 사교육을 제공받고 있다. J.-H. Lee와 Han (2019)은 3-5세 유아를 위한 수학 교육 방법 중 교사가 가정으로 방문하는 학습지를 이용하는 경우는 20.5%, 수학 전문학원을 다니는 경우는 3.1%였다고 보고하였다. 보다 최근 자료(Kang & Im, 2023)에 따르면, 연령을 4, 5세로 좁혔을 때 학습지 혹은 학원을 이용해 수학 사교육을 이용하는 유아의 비율은 41.7%로 나타났다. 이처럼 상당 비율의 유아가 학령 전기부터 수학 사교육에 노출되고 있음에도 불구하고, 수학 사교육에 대한 연구는 주로 사교육 현황이나 부모 및 교사의 사교육에 대한 인식을 파악하는 정도에 머무르고 있다(J.-H. Lee & Han, 2019; Woo, Kim, & Baek, 2005). 따라서 우리나라의 특수한 사회문화적 현상을 고려했을 때, 부모의 수학 기대가 수학 학습 기회를 제공하는 데 미치는 영향을 검토하는 데 있어 가정수학활동 뿐 아니라 부모의 사교육에 대한 의존도를 포괄하여 종합적으로 살펴보아야 할 필요성이 대두된다. 부모가 자녀의 학업성취 수준에 대해 높은 기대를 가질수록 수학과 관련된 사교육을 더 많이 시키는 경향이 있다는 선행연구(E. Kim, Choi, Choi, & Jang, 2016; Min & Bae, 2014)는 이러한 필요성을 뒷받침한다.
본 연구는 부모의 수학 기대가 가정수학활동 및 수학 사교육 의존도에 미치는 영향에 대해 종합적으로 분석해보고자 한다. 이때 가정수학활동은 난이도에 따라 기본수학활동과 고급수학활동으로 구분해 살펴볼 것이다. 뿐만 아니라, 본 연구는 실제로 가정수학활동이나 수학 사교육 의존 정도가 유아의 수학 능력에 영향을 미치는지 살펴봄으로써, 매개관계가 유의하게 나타나는지 알아볼 것이다. 이를 통해 수학 기대가 높은 부모들은 어떤 유형의 수학 학습 기회를 자녀에게 제공하고 있으며, 그 중 어떤 유형의 수학 학습 방식이 유아기 자녀의 수학 능력 향상에 실질적으로 도움을 주고 있는지 파악하고자 한다. 본 연구의 결과는 유아들의 수학 능력 향상을 위한 교육환경 구성을 위한 실용적 함의를 제공할 수 있을 것으로 기대된다.
한편, 본 연구에서는 유아의 수학 능력을 수 개념과 수학적 문제해결력으로 구분해 살펴보고자 한다. 수 개념(numeracy)이란 사물의 수량, 부피, 크기와 같은 속성에 대해 생각하는 방법으로, 순차적·조직적 사고 방법을 의미한다(G. Lee, Hong, Shin, & Jin, 1997). 유아들은 수 개념에 대한 이해를 갖고 있으며 연령의 증가에 따라 수 개념 관련 능력이 향상된다. 한국 유아를 대상으로 한 연구를 예로 들면, 3세쯤 3을 정확히 알고 있으며, 5 정도 수준에서 더하기나 빼기를 하려는 시도가 나타난다. 4세의 경우 5이하 수에서 더하기 및 빼기를 하기 위한 시도를 보다 분명하게 하며, 5세가 되면 5에서 10까지 수에서의 더하기나 빼기를 위한 시도를 할 뿐 아니라 정확한 답을 얻어내는 모습을 볼 수 있다(Shin, 2000). 그러나 유아의 수학 능력에 대한 선행연구는 전통적으로 수 개념 발달에 초점을 두어, 수 세기나 수 연산과 같은 영역에 치중된 경향이 있다(Rittle-Johnson, Fyfe, Loehr, & Miller, 2015). 물론 수 개념은 고급 수학 능력의 토대가 되는 기본 능력이기는 하지만(Purpura & Lonigan, 2015) 다양한 영역의 수학 능력을 포괄한 연구가 부족하다는 점이 한계로 지적되었다.
최근에는 유아기의 수학적 문제해결력에 대한 학자들의 관심이 높아지고 있는데(Yang & Kim, 2019), 수학적 문제해결력은 수학적인 소양 및 지식을 바탕으로 수학적 내용에 대해 이해하고 일상에서 만나는 수학적 문제를 해결할 방법을 찾고 활용할 수 있는 능력으로 정의된다(M.-J. Kim & Yi, 2021). 수학적 문제해결력은 단순히 수학적 개념을 이해하는 데서 나아가 실질적 문제를 해결하는 방안을 찾아내는 데까지 확장된 개념이기 때문에 수 개념 발달에 비해 범위가 더 넓으며 난이도가 더 높은 영역이라고 볼 수 있다(Li et al., 2020). 수학적 문제해결력은 수 개념을 기반으로 하기 때문에, 연령에 따라 발달 정도가 향상될 것임을 추측해볼 수 있다. 본 연구는 유아의 수학 능력을 수 개념과 수학적 문제해결력으로 구분해 검토해 봄으로써, 가정 수학환경이나 사교육 의존도와 같은 변인의 영향력이 유아의 수학 능력에 미치는 영향력을 더욱 세분화해 살펴보고자 한다. 이상의 논의를 토대로 도출한 연구문제는 다음과 같다.
연구문제 1
유아의 월령, 수용 어휘력, 부모의 사회경제적 지위를 통제했을 때, 부모의 수학 기대는 유아에게 제공하는 가정수학활동(기본, 고급) 빈도를 유의하게 예측하는가?
연구문제 2
유아의 월령, 수용 어휘력, 부모의 사회경제적 지위를 통제했을 때, 부모의 수학 기대는 유아기 수학 사교육에 대한 의존도를 유의하게 예측하는가?
연구문제 3
유아의 월령, 수용 어휘력, 부모의 사회경제적 지위를 통제했을 때, 부모의 수학 기대와 유아의 수학 능력(수 개념, 수학적 문제해결력)의 관계는 가정수학활동(기본, 고급) 및 수학 사교육 의존도에 의해 유의하게 매개되는가?
Methods
연구대상
연구대상은 서울, 경기도, 충남, 경북 지역의 유치원에 재학하는 4, 5살 유아 297명(M = 59.18, SD = 5.47, Range = 48∼72개월)과 그들의 부모다. 연구참여에 동의한 총 10개 유치원의 25개의 학급에 재학 중인 유아와 그들의 부모를 대상으로 조사가 이루어졌으며, 한 교실에서 평균 11.8명의 유아가 참여하였다(Minimum = 1, Maximum = 20). 다양한 사회·경제적 배경을 가진 유아와 그들의 부모를 대상으로 하고자 지역별로 중산층과 저소득층이 거주하는 지역에 위치하는 유치원을 골고루 표집하였다. 자료수집에 참여한 유아 299명 중 결석 등의 이유로 참여하지 못한 유아 2명을 제외하고 최종 297명의 유아와 부모의 자료를 사용하였다.
이 연구가 대상을 4, 5세 유아로 한정한 것은 수 개념을 비롯한 유아기의 수학적 능력은 연령의 증가에 따라 향상되는데(Shin, 2000), 특히 수 비교 능력의 변화가 3세와 4세 사이에 두드러지며 4, 5세 사이에는 비교적 안정된다는 선행연구에 근거한다(Cho & Yi, 2017). 뿐만 아니라, 본 연구에서 주요하게 다루는 변수인 가정수학활동과 수학 사교육 의존도 역시 연령의 증가와 함께 수준이 높아지는 변인으로 보고된다(Kang & Im, 2023; Thompson, Napoli, & Purpura, 2017). Tompson 등(2017)에 따르면, 가정에서 수학활동을 제공하는 빈도가 3세에 비해 4세에 더 높게 나타나며, 가정수학활동을 고급활동과 기본활동으로 나누었을 때 유아의 수학능력과의 관련성 차이가 3세에는 관찰되지 않지만 4세에서는 유의하게 나타난다. 이러한 결과를 종합적으로 고러하여, 연구의 신뢰성 및 타당성을 확보하기 위해 연구 대상을 유아기 중 4, 5세로 한정하였다.
연구도구
유아의 수학 능력
수 개념 유아의 수 개념 발달은 Purpura, Reid, Eiland, 그리고 Baroody (2015)가 개발한 표준화된 검사 도구 (Preschool Early Numeracy Skills-Brief Test [PENS-B])를 사용해 측정하였다. PENS-B는 총 25문항으로 이루어졌으며, 유아의 수 개념 발달과 관련된 내용(예: 숫자 인식, 일대일 대응, 수 감각, 수량 비교, 수 연산)을 포괄적으로 포함한다. 검사는 훈련된 검사자가 면담을 통하여 유아에게 검사지의 내용을 질문하고, 유아의 응답을 기록하는 방식으로 1명의 유아 당 10분 이내에 이루어졌다. 검사 내용의 예를 들면, 검사자가 세 개의 점이 그려져 있는 그림을 손가락으로 짚으면서 유아에게 “이 점들을 손가락으로 하나하나 가리키면서 세어 보자.”라고 하기도 하며, 강아지 세 마리와 자동차 두 대가 있는 그림을 보여주면서 “여기 강아지가 몇 마리지?”라고 질문하기도 한다. 검사자는 유아에게 응답 기회를 3번까지 제공하며, 유아가 3번째 기회에도 정답을 맞히지 못하면 0점 처리하였다. PENS-B 총점은 0점에서 25점 사이이며, 점수가 높을수록 유아의 수 개념이 높다고 해석할 수 있다. PENS-B의 내적 신뢰도는 .89이다.
수학적 문제해결력 유아의 수학적 문제해결력은 WoodcockJohnson Ⅲ Applied Problem (Woodcock, McGrew, Mather, & Schrank, 2001)를 사용해 측정하였다. 본 도구는 유아의 양적 추론(quantitative reasoning), 수학 성취도(math achievement), 수학 지식(math knowledge)을 검사하기 위한 도구이다. 검사는 훈련된 검사자가 유아에게 수학적 문제상황이 있는 그림을 보여주고 유아가 종이와 연필을 활용하여 문제를 해결하는 방식으로 이루어진다. 문제는 그림과 도표, 데이터 테이블을 보고, 유아가 수학적 지식을 활용해 해결하도록 구성되어 있다. 본 도구는 유아부터 초등학생까지 사용할 수 있으며, 난이도 순서에 따라 문제가 배열되어 있다. 즉 쉬운 문제가 먼저 제시되어 있으며, 문제의 난이도가 갈수록 높아진다. 유아가 연속해서 세 문제 이상 맞히지 못하면 검사가 종료된다. 예를 들어, 7개의 동전이 있는데, 3개를 사용하면 몇 개의 동전이 남을지 예측해 보도록 하는 문제가 제시된다. 본 연구에서 신뢰도 점수는 .85이다.
부모의 수학기대
부모의 수학 기대는 Kleemans, Segers와 Verhoeven (2013)이 개발한 Parents’ numeracy expectation를 활용해 측정하였다. 이 척도는 부모에게 유아가 유치원을 졸업할 무렵 어느 정도 수학 능력을 갖추기를 기대하는지를 묻는 7개 문항으로 구성된다. 질문의 예로는 “자녀가 유치원을 졸업할 무렵 1에서 20까지 수 세기를 완벽하게 숙달할 것을 기대하는지?” 등을 알아보는 내용이 있다(Table 1). 본 척도는 4점 리커트 척도를 활용하였으며, 응답 범위는 1은 전혀 숙달하지 못함, 2는 조금 숙달, 3은 충분히 숙달, 4는 완벽히 숙달이다. 본 척도의 점수가 높을수록 부모가 유아기 자녀에게 높은 수학적 성취를 기대한다고 볼 수 있다. 이 도구 전체의 신뢰도(Cronbach’s α)는 .92이다.
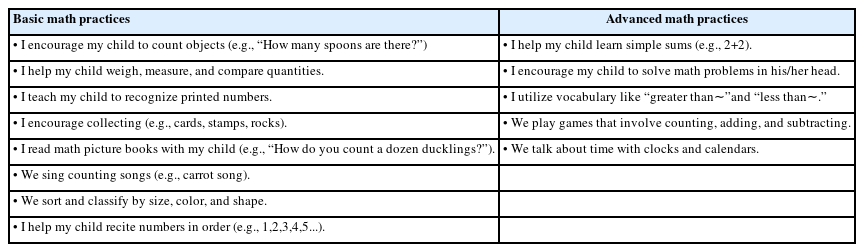
난이도에 따른 가정수학활동
본 연구에서는 Skwarchuk, Sowinski, & LeFevre (2014)과, Girard 등(2023)의 연구에 기초하여 부모와 함께 하는 가정수학활동을 난이도에 따라 다음 두 가지로 분류하였다.
기본수학활동(basic math practices) 기본수학활동은 부모와 유아가 간단하게 숫자를 세거나 수와 관련된 동화책을 읽고, 노래 부르는 것과 같은 단순한 수학활동을 의미한다(Skwarchuk et al., 2014). Table 2와 같이, 기본수학활동 척도는 부모와 유아가 함께 하는 단순한 수학활동에 대한 8개의 문항으로 이루어졌다. 기본수학활동 빈도를 알아보기 위해 5점 리커트 척도를 활용해 측정하였으며, 한 번도 안 함은 1, 한 달에 1번은 2, 일주일에 1번은 3, 일주일에 3-4번은 4, 매일은 5로 구성되었다(Cronbach’s α = .76).
고급수학활동(advanced math practices) 고급수학활동은 유아가 수학적으로 사고할 수 있도록 자극하는, 기본수학활동보다 어려운 수학활동이다(del Río et al., 2017). 예를 들어, 부모는 유아에게 머릿속으로 수 연산을 하도록 장려하는 것과 같이 더 정교한 방법을 사용할 수 있다. 고급수학활동 척도를 구성하는 문항의 예는 Table 2에 제시되었다. 고급수학활동 빈도를 알아보기 위해 5점 리커트 척도를 활용해 측정하였으며, 한 번도 안 함은 1, 한 달에 1번은 2, 일주일에 1번은 3, 일주일에 3-4번은 4, 매일은 5로 구성되었다(Cronbach’s α = .77).
수학 사교육 의존도
수학 사교육 의존도란, 부모가 유아기 자녀의 수학 학습을 위한 방법으로 학습지나 학원과 같은 사교육에 의존하는 정도를 의미한다. 즉, 수학 사교육 의존도가 높은 부모는 수학 사교육 방법을 선호하며 실제로 많이 활용하고 있는 부모를 의미한다. 본 연구에서 사용한 척도는 Park (2011)의 사교육 참여 문항을 참고로 하여 구성되었으며, 5개의 문항으로 이루어진 부모 보고식 질문지이다. 먼저 학습지의 필요성과 효과성에 대한 부모의 인식을 확인하기 위해 자녀에게 수학을 가르치기 위해 학습지를 이용하는 것이 얼마나 필요한지, 또 얼마나 효과적이라고 생각하는지 질문하였다. 이 문항에 대한 응답은 5점 척도로 1번은 전혀 그렇지 않다, 2번 그렇지 않은 편이다, 3번 보통이다, 4번 그런 편이다, 5번은 매우 그렇다로 구성되었다. 다음으로 부모가 생각하는 유아기 수학 교육을 위한 방법의 우선 순위를 조사하였다. 이 문항에서 부모가 1, 2 순위로 학습지와 학원을 선택할 경우 가장 높은 점수를 부여하였으며(5점), 1, 2 순위로 학습지나 학원 중 하나를 선택했을 때는 3점, 1, 2 순위로 학습지나 학원을 모두 선택하지 않고 부모가 가르치거나, 따로 하는 것이 없을 경우 0점을 부여하였다. 그 외에 유아가 학습지를 시작한 연령에 대한 주관식 응답을 역코딩하여 6살부터 시작하였으면 1점을 부여하였으며, 1살부터 시작하였으면 6점을 부여하였다. 마지막으로 수학 사교육비용에 얼마를 투자하는지 알아보기 위하여 5점 척도를 사용하였다. 1은 전혀 돈을 쓰지 않는다, 2는 5만원 이하, 3은 5-10만원, 4는 10만원 이상으로 코딩되어, 사교육에 비용을 많이 사용할수록 높은 점수를 부여하였다. 수학 사교육 의존도 문항의 신뢰도 계수는 .66이었다.
통제변인
본 연구는 통제변인으로 유아의 월령, 유아의 수용어휘력, 그리고 부모의 사회경제적 지위를 활용하였다. 유아의 연령에 따라 가정수학활동이 달라질 수 있다는 선행연구(Thompson et al., 2017)를 바탕으로, 본 연구에서는 유아의 월령을 통제하였다. 유아의 수용어휘력은 유아의 어휘력 검사 (Receptive and Expressive Vocabulary Test [REVT]; Y.-T. Kim, Hong, & Kim, 2009)를 사용해 측정하였다. 본 연구에서는 유아가 언어발달과 수학성취의 상관관계에 대한 선행연구를 바탕으로(Napoli & Purpura, 2018), 유아의 인지발달, 이해력 등을 통제하고자 유아의 수용어휘력을 통제 변인으로 사용하였다. 수용어휘력 검사는 명사, 동사, 형용사, 부사로 이루어져 있으며, 총 185문항이다. 유아는 훈련된 검사자가 말하는 어휘를 듣고 4장의 그림 중 가장 적절하다고 생각하는 그림을 선택한다. 유아의 응답이 맞으면 1점, 틀리면 0점으로 채점되어 점수가 높을수록 수용 어휘력이 높다는 것을 의미한다. 부모의 사회경제적 지위가 유아의 수학성취를 예측한다는 선행연구(Muñez, Bull, & Lee, 2021)를 기초로 하여, 최종학력과 가구 월수입 변수를 활용해 잠재 변수를 만들어 투입하였다. 부모의 최종학력은 고졸 이하, 전문대졸, 4년대 졸, 석사학위 이상으로 범주화되었으며, 가구 월 소득은 200만원 이하, 200만원∼300만원, 300만원∼400만원, 400만원∼500만원, 500만원∼600만원, 600만원 이상으로 범주화하였다.
연구절차
본 연구에서 부모 변인은 부모 설문지를 통해 수집하였으며, 유아의 수 개념, 수학적 문제해결력, 수용 어휘력의 경우 유아 대상 검사를 통해 자료를 수집하였다. 유아의 집중력을 포함한 발달 단계를 고려하여 유아 검사는 각각 다른 날짜에 수행하였으며, 각각의 검사에 걸리는 시간은 10분 내외였다. 검사의 순서는 무작위로 배정하였다. 본 연구에서 사용된 국외 연구척도는 번역과정에서 문항 타당성을 확보하기 위하여 세 단계를 거쳤다. 첫째, 유아교육 전문가 2인이 일차 번역을 하였다. 둘째, 미국대학의 유아교육과 교수 1인이 영어 원문과 번역본을 검토하여, 문항의 일부를 수정하고 보완하였다. 셋째, 문항의 내용이 명확하게 전달되는지 확인하기 위해 2-3명의 유아를 대상으로 예비조사를 실시하였다. 연구자는 유아의 연령에 맞는 검사방법을 비디오로 촬영하여 대학원생을 훈련하였다. 검사자 간 신뢰도를 확보하기 위하여 유아 모의 검사 훈련을 반복적으로 거쳤으며, 3명의 훈련된 검사자들은 10개의 대상 유치원을 방문하여 유아 검사를 실시하였다. 유아 검사는 유치원 일과 중에서 조용하고 편안한 공간에서 개별 유아와 1:1로 이루어졌다.
자료분석
기초통계와 Pearson 상관분석 시행을 위하여 SPSS 19 (IBM Co., Armonk, NY)를 사용하였으며, 측정변수의 총합을 활용하였다. 부모의 수학 기대, 기본 및 고급 가정수학활동, 그리고 수학 사교육 의존 정도가 유아의 수 개념 및 수학적 문제해결력에 미치는 영향력을 알아보기 위하여 Mplus 7.0 (Muthén & Muthén, Los Angeles, CA)을 사용하여 구조방정식 모형 분석을 실시하였다. 구조 방적식 모형에서 측정모형을 더 정확하게 설정하고, 모형 적합도를 높이기 위하여 고유분산 고립 방법에 기초한 문항 묶음(item parcel)을 활용하였다(J. Lee & Kim, 2016; Little, Rhemtulla, Gibso, & Schoemann, 2013). 사용하는 지표변수가 모두 정규성 가정을 만족시키고 있으므로 최대우도법(Maximum Likelihood Estimation [ML])을 활용하여 구조방정식 모형을 분석하였다. 마지막으로 매개 효과의 유의성을 검증을 위하여 bootstrapping을 10,000번 실시하였다. bootstrapping은 주어진 데이터로부터 복원 표본을 구하는 작업을 여러 번 반복하여 신뢰구간 안에서 경로계수를 정밀하게 추정하는 기법이다(Kline, 2011).
Results
상관관계
본 연구에서는 변인들 간의 관계를 확인하기 위하여 기술통계 및 상관관계 분석을 실시하였다. 그 결과를 Table 3과 같이 제시하였다.
변수 간의 상관관계를 보면, 부모의 수학 기대는 고급수학활동과 정적 상관관계(r = .23, p < .001), 기본수학활동과 정적 상관관계가 있었으며(r = .17, p < .01), 수학 사교육 의존도와도 정적 상관이 있었다(r = .16, p < .01). 또한 고급수학활동은 유아의 수 개념 발달과 정적 상관관계가 있었으며(r = .34, p < .001), 수학적 문제해결력과도 정적 상관이 있었다(r = .32, p < .001). 기본수학활동도 유아의 수 개념 발달과 정적 상관이 있으나(r = .14, p < .05), 수학적 문제해결력과는 유의한 상관이 나타나지 않았다(r = .11, p > .05). 반면에 수학사교육에 대한 의존도는 수 개념 발달과 관계가 없으며(r = -.05, p > .05), 수학적 문제해결력과도 상관이 없다(r = -.06, p > .05).
연구모형 검증
본격적인 분석에 앞서 활용된 변수의 왜도와 첨도를 확인해 본 결과 각각 절대값이 2와 7을 넘지 않아 정규성 분포를 만족하였다. 또한 본 연구에서 분석한 연구모형의 적합도는 CFI = .93, TLI = .91, RMSEA = .07, SRMR = .07로 모두 적합도가 높은 것으로 나타났다.
Figure 1은 구체적인 구조방정식 분석 결과를 보여준다. 두 개의 선으로 표시된 경우. 부분 매개가 이루어졌다. 즉, 고급수학활동은 부모의 수학 기대와 유아의 수 개념 발달을 매개하였다. 또한, 고급수학활동은 부모의 수학 기대와 유아의 수학적 문제해결력을 매개하였다. 그러나 기본수학활동과 수학 사 교육에 대한 의존도는 부모의 수학 기대와 유아의 수 개념 발달이나 수학적 문제해결력의 관계를 매개하지 못하였다.

Structural equation modeling predicting children’s math achievement.
*p < .05. **p < .01. ***p < .001.
Table 4에는 직접 효과와 간접 효과를 비표준화된 계수, 비표준화된 계수의 오차, 표준화된 계수로 제시하였다. 통제변인 관련 결과를 먼저 자세히 살펴보면(Table 4), 유아의 월령은 유아의 수 개념 발달(β = 25, p < .001)과 유아의 수학적 문제해결력 (β = 18, p < .001)을 모두 유의미하게 예측하였다. 또한 유아의 수용 어휘력은 유아의 수 개념 발달(β = 07, p < .001)과 유아의 수학적 문제해결력 (β = 10, p < .001)을 모두 유의미하게 예측하였다. 부모의 사회경제적 지위는 부모의 수학 기대를 예측하지 못하였지만(β = 06, p > .05), 사교육에 대한 의존도를 부적으로 예측했다(β = -.27, p < .001).
다음으로 연구문제와 관련된 내용을 구체적으로 살펴보면(Table 4), 부모의 수학 기대는 고급수학활동(β = 12, p < .01)과 기본수학활동(β = 30, p < .001)을 모두 예측하지만, 사교육에 대한 의존도는 예측하지 못한다(β = .06, p > .05). 또한 고급수학활동은 유아의 수 개념 발달(β = 5.93, p < .001)과 수학적 문제해결력(β = 4.74, p < .001)을 모두 예측한다. 반면에 기본수학활동은 유아의 수 개념 발달(β = -.76, p > .05)과 수학적 문제해결력(β = -.66, p > .05)을 모두 예측하지 못한다. 사교육에 대한 의존도 역시 유아의 수 개념 발달(β = -.24, p > .05)과 수학적 문제해결력(β = -.21, p > .05)을 모두 예측하지 못한다.
Table 5에는 잠재변수 간 직접 효과, 간접 효과, 총 효과를 정리하였다. 내용을 자세히 보면, 고급수학활동은 유아의 수 개념 발달에 통계적으로 유의한 효과가 있으며(β = .71, p < .01), 고급수학활동은 유아의 수학적 문제해결력에 대한 간접 효과도 통계적으로 유의하다(β = .59, p < .01).
Table 3에서 제시된 간접 효과의 유의성을 정밀하게 검증하기 위해 bootstrapping을 실시하였다. bootstrapping은 간접 효과의 표준오차를 무선으로 표집하여 10,000회 반복하여 돌려 경로계수의 신뢰구간을 확인하는 방법이다(Preacher & Hayes, 2004). 구조 모형의 각 경로계수를 Table 6에 제시하였다. 이를 자세히 살펴보면, 가정 고급수학활동은 유아의 수 개념과 수학적 문제해결력을 유의하게 매개하고 있다. 먼저, 유아의 수 개념으로 가는 경로계수의 95% 신뢰구간이 .11에서 1.83로 0을 포함하고 있지 않다. 마찬가지로 유아의 수학적 문제해결력으로 가는 경로계수의 95% 신뢰구간은 0.09에서 1.66으로 0을 포함하고 있지 않다. 따라서 가정 고급수학활동은 부모의 수학 기대와 유아의 수 개념 발달, 수학적 문제해결력을 유의하게 매개하고 있다.
Discussion
이 연구는 부모의 수학 기대가 가정수학활동 빈도 및 수학 사교육 의존도를 예측하는지 알아보았다. 또한, 부모의 수학 기대가 유아의 수학 능력에 미치는 효과를 가정수학활동 및 수학 사교육 의존도가 유의하게 매개하는지 추가로 검토하였다. 이때 가정수학활동은 기본수학활동과 고급수학활동으로 나누어 난이도에 따라 구분하였으며, 유아의 수학 능력은 수 개념과 수학적 문제해결력으로 나누어 살펴보았다. 연구결과를 기반으로 한 주요 논의 사항은 다음과 같다.
첫째, 부모의 수학 기대는 가정에서 제공하는 기본수학활동과 고급수학활동을 모두 예측하였다. 즉, 유아기 자녀의 수학성취에 대한 기대 수준이 높을수록 부모는 가정에서 유아기 수준의 수학활동뿐 아니라 조금 더 난이도가 높은 수학활동도 높은 빈도로 제공하고 있었다. 이러한 결과는 부모가 자녀의 학업성취에 대한 기대를 높게 가질수록 가정에서 가정수학활동을 더 많이 제공하는 경향이 있다고 보고한 선행연구들(Im et al., 2019; Susperreguy et al., 2020)과 맥을 같이한다. 뿐만 아니라, 가정수학활동을 기본수학활동 및 고급수학활동으로 나누어본 경우에도 유사한 결과가 나타남을 보고한 선행연구(Skwarchuk et al., 2014)와도 결과가 일치한다. 이러한 결과는 자녀의 수학 능력에 대한 기대를 높게 가질수록 자녀에게 수학적 상호작용을 제공하게 되는 동기가 높아지기 때문인 것으로 보인다(Kleemans et al., 2018). 다시 말해, 자녀의 수학 성취에 대한 기대가 높은 부모는 자녀에게 수학적 자극을 제공하고자 하는 높은 동기로 인해 다양한 난이도의 수학적 상호작용을 풍부하게 제공하는 것으로 추측된다.
둘째, 부모의 수학 기대는 수학 사교육 의존도를 유의하게 예측하지 못했다. 부모의 수학 기대가 높을수록 자녀에게 수학 학습 기회를 많이 제공하는 경향이 있기 때문에(Kleemans et al., 2018), 수학 사교육에 대한 의존도도 높게 나타날 것이라 예상하였으나 실제 결과는 그렇지 않았다. 부모의 수학 기대 수준이 가정에서 이루어지는 수학활동의 빈도를 예측한다는 본 연구의 결과와 비교해 보았을 때, 부모의 수학 기대가 수학 사교육 의존도를 예측하지는 못한다는 결과는 더욱 흥미롭다. 즉, 유아기 자녀에 대한 수학 기대가 높은 부모는 수학 사교육에 의존하기 보다는 가정에서 수학적 자극을 더욱 풍부하게 제공해주고 있었다. 유아기의 수학 사교육 의존은 특수한 사회문화적 현상으로 볼 수 있기 때문에 관련 선행연구가 제한적이다. 따라서 이러한 결과를 해석하는 데 있어 충분한 근거자료를 얻기 어렵지만, 자녀의 수학 능력에 대한 부모의 기대감보다는 자녀교육에 대한 불안감이나 동조심리가 사교육 의존도와는 더 밀접한 관련이 있는 변인일 가능성이 있다. 실제로 초등학생 부모를 대상으로 한 연구에서는 자녀교육에 대한 관심, 불안심리 및 동조심리가 강할수록 지출하는 사교육비가 높아짐을 밝힌 연구가 있다(H. Kim, 2004). 그러나 이는 초등학생 자녀를 대상으로 한 연구이기 때문에 유아기에 적용하기에는 한계가 있으며, 유아기 자녀를 대상으로 한 연구가 필요하다.
셋째, 부모의 수학 기대와 유아의 수학 능력의 관계를 가정에서 이루어지는 기본수학활동이 유의하게 매개하지 못했다. 즉, 부모의 수학기대는 가정에서의 기본수학활동을 정적으로 예측하였지만, 기본수학활동을 많이 한다고 해서 유아의 수 개념이나 수학적 문제해결력에 높아지는 것은 아니었다. 이러한 결과와 비교해, 가정에서 이루어지는 고급수학활동은 부모의 수학 기대와 유아의 수학 능력의 관계를 유의하게 매개하였다. 즉, 부모의 수학 기대가 높은 것은 가정에서 빈번한 고급수학활동을 제공하는 데 영향을 미치게 되며, 이러한 고급수학활동이 실제로 유아의 수 개념이나 문제해결력과 같은 수학 능력을 높이는 데 효과가 있었다. 가정에서 이루어지는 기본 수학활동보다는 고급수학활동이 유아의 수학 능력을 높이는 데 더욱 강력한 요인이 된다는 결과는 선행연구에서도 일치하는 결과가 상당 수 보고되었다(Girard et al., 2023; Gunderson & Levine, 2011; Skwarchuk et al., 2014). 예를 들어, Guderson과 Levine (2011)은 부모와 유아가 작은 수 세기를 함께하는 것보다는 큰 수 세기를 함께하는 것이 자녀의 수학 능력 발달에 더 도움이 되는 활동임을 보고하였다.
고급수학활동이 기본수학활동보다 유아의 수학 능력에 더 강력한 영향력을 미친다는 결과는 사회문화적 구성주의 이론의 근접 발달영역을 통해 설명 가능하다. 근접 발달영역이란, 아직 달성하지는 못했지만 적절한 비계설정이 주어진다면 달성 가능한 영역을 의미한다(Vygotsky, 1978). 기본수학활동은 기존의 유아가 갖고 있는 수학 능력의 수준 정도에 해당하기 때문에 기본수학활동을 더 많이 제공한다고 해도 수학 능력이 더욱 향상되는 효과는 기대하기 어려울 수 있다. 이에 비해, 고급수학활동은 유아의 현재 수준보다 조금 더 높은 수준의 활동에 해당하며, 고급수학활동을 풍부하게 제공하는 것이 비계의 역할을 함으로써 유아의 수 개념 및 수학적 문제해결력과 같은 수학 능력을 향상시키는 데 효과적이었던 것으로 해석된다. 고급수학활동을 할 때 유의할 사항은, 부모는 유아의 현재 발달 상태를 면밀히 파악하여 현재의 수준보다 약간 더 높은 수준의 상호작용을 제공해야 한다는 점이다. 과도하게 심화된 수학적 상호작용을 제공해 지나친 선행학습을 기대하는 것은 오히려 역효과가 있을 수 있다.
넷째, 가정에서의 고급수학활동은 부모의 수학 기대와 유아의 수학 능력을 유의하게 매개하였는데, 이때의 직접효과 역시 유의해 부분매개효과가 확인되었다. 즉, 부모의 수학 기대가 높을수록 유아의 수 개념 및 수학적 문제해결력이 높은 것은 부분적으로 가정에서 고급수학활동을 높은 빈도로 제공하기 때문인 것으로 설명되지만 여전히 설명되지 않은 부분이 남아 있다. 이러한 결과는 부모의 수학 기대와 유아의 수학 능력의 관계를 가정에서 제공하는 수학활동이 부분적으로 매개함을 밝힌 선행연구(Im et al., 2019)의 결과와 일치한다. Im 등(2019)은 우리나라 유아들은 사교육에 이른 시기 노출되기 시작하기 때문에 수학 사교육과 같은 요인이 설명되지 않은 부분을 설명할 변수가 될 수 있다는 가능성을 제안하였다. 부모가 자녀의 학업성취에 대한 기대를 높게 가질수록 수와 관련한 사교육을 많이 시키고(E. Kim et al., 2016; Min & Bae, 2014), 사교육 경험이 유아의 수학 능력에 유의한 영향을 줄 수 있기 때문이다. 그러나 본 연구에서 실제로 수학 사교육 의존도를 연구모형에 투입해 가정수학활동 변인과 함께 분석해 보았지만, 여전히 부모의 수학 기대와 유아의 수학 능력 간의 관계는 고급수학활동이 부분매개함을 확인하였다.
후속연구에서는 부모의 수학 기대가 유아의 수학 능력에 미치는 영향력을 설명할 수 있는 추가적인 매개변인에 대한 탐색이 이루어질 필요가 있다. 예를 들면, 유아기 자녀에게 적합한 수학교육 방법에 대한 이해 수준 같은 변인을 고려해볼 수 있다. 즉, 부모의 수학 기대가 높은 경우 유아기 자녀의 발달 수준에 맞는 수학교육방법에 대한 정보를 적극적으로 수집하여, 유아에게 더욱 접합한 방식으로 상호작용을 제공했을 가능성이 있다(DeFlorio & Beliakoff, 2015). 혹은 본 연구에서 다루지 못한 부모나 유아의 지능 점수와 같은 변인(Chu, van Marle, & Geary, 2015)을 고려한 연구모형을 검토해본다면 다른 결과가 도출될 가능성이 있어, 추후 연구를 통해 규명할 필요가 있다.
본 연구의 한계는 다음과 같다. 첫째, 가정수학활동을 보다 세밀하게 나누어 검토할 필요가 있다. 본 연구는 가정수학활동을 기본활동과 고급활동으로 나누어 난이도에 따라 검증하였다. 그러나 선행연구에 따르면, 가정수학활동을 명시적으로 수학적 개념을 가르치고자 하는 의도가 있는 형식적 활동(예: 수 세기, 더하기)과 수학을 가르치고자 하는 의도 없이 수학적 내용을 함축하는 놀이(예: 보드게임, 요리 등)인 비형식적 활동으로 구분했을 때 유아의 수학 능력에 미치는 영향력이 다르게 나타나기도 한다(Girard et al., 2023; LeFevre et al., 2009). 따라서 가정수학활동의 특성을 다양한 기준으로 나누어 분석해 보는 시도가 필요하다. 둘째, 가정수학활동의 빈도를 질문지로 측정하였기 때문에 생태학적 타당도를 보장하는 데 한계가 있다. 즉, 질문지를 이용한 응답은 사회적으로 바람직하다고 여겨지는 방향으로 응답할 가능성을 높이기 때문에, 실제 생활에서 이루어지는 부모-자녀 간의 상호작용을 파악하는 데 한계가 있을 수 있다. 따라서 일상적으로 이루어지는 가정수학활동에 대한 자료를 더욱 신뢰롭고 타당하게 측정할 수 있는 방법의 도입이 필요하다.
또한, 본 연구는 횡단데이터에 근거하고 있기 때문에 명확한 인과관계를 밝히기 어렵다. 본 연구의 모형은 자녀의 수학 능력에 대한 기대가 높을수록 수학학습의 기회를 많이 제공하며, 이로 인해 자녀의 수학 능력이 높아질 것이라는 가정에 기반하고 있으나 이러한 방향성은 양방향적이기 때문에 다르게 해석될 가능성이 있다. 예를 들면, 실제로 자녀의 수학 능력이 높은 경우 부모가 자녀의 수학 능력에 대한 기대를 더 높게 가지고 수학 학습의 기회를 더 많이 제공할 가능성도 있는 것이다. 따라서 변인들 간의 양방향적 관계에 유의하여 연구 결과를 해석할 필요가 있다. 마지막으로, 본 연구에서 다룬 가정수학활동이나 수학 사교육 외에도 유아의 수학적 사고를 자극할 수 있는 교육 요소에 대한 추가적인 검토가 필요하다. 예를 들어, 유치원이나 어린이집과 같은 기관 역시 유아들에게 수학적 교육환경을 제공하는 주요한 역할을 수행하고 있다(Chung, 2001; S.-R. Kim, Hong, Kim, & Hong, 2008). 따라서 수학 사교육 의존도뿐 아니라 가정수학활동이 유아교육기관에서 이루어지는 수학 활동과 어떠한 복합적 관계를 통해 유아의 수학 능력에 영향을 미치는지에 대한 연구가 이루어질 필요가 있음을 제안한다.
위와 같은 한계점에도 불구하고 본 연구는 유아기 자녀를 양육하는 부모들에게 실용적 함의를 제공한다. 즉, 부모의 수학 기대가 높을수록 유아의 수 개념 및 수학적 문제해결력과 같은 수학 능력이 높게 나타나는 것은 사교육에 대한 의존도보다는 가정에서 이루어지는 부모와의 수학적 상호작용을 통해 설명된다는 점을 밝혔다. 특히 유아의 현재 발달 수준보다 약간 앞선 수준의 고급 내용을 다루는 수학적 상호작용이 유아의 수학 능력 향상에 더욱 도움이 되는 변수였다. 따라서 가정에서는 사교육에 대한 지나친 의존보다는 부모-자녀 상호작용을 통한 수학적 놀이와 활동을 풍부하게 제공할 것을 권고할 수 있다. 이러한 결과는 가정에서 유아의 수학 능력 발달에 도움을 주기 위해 부모가 비계 제공을 하는 역할이 중요함을 시사한다. 마지막으로 이 연구는 가정수학활동에 대한 국내 연구가 미흡한 상황에서 국외 연구들을 토대로 우리나라의 상황을 고려한 연구를 수행함으로써, 관련 연구의 확장을 위한 기여를 하였다는 점에서 이론적 의의가 있다.
Notes
This article was presented at the 2023 Annual Spring Conference of Korean Association of Child Studies.
Conflict of Interest
No potential conflict of interest relevant to this article was reported.